ロジカルシンキングとは、物事を論理的に考える思考法のことです。
日常生活、ビジネスシーンのどちらにも活用できる思考法で、問題解決能力が向上したり、合理的思考が身についたりするメリットがあります。
本記事では、ロジカルシンキングの手法のひとつである演繹法（えんえきほう）の特徴や使い方、例題などを紹介します。
ロジカルシンキングについて勉強中の方、演繹法や帰納法を仕事に活かしたい方に当てはまる方におすすめの記事となっていますので、ぜひ参考にしてみてください。
書籍『リーダーの仮面』の図説資料をプレゼント！
株式会社識学 代表取締役社長 安藤広大の執筆した書籍「リーダーの仮面」は、結果の出せるリーダーになるために必要なテクニックをまとめたリーダーシップ本の決定版！
誰でも実践できるマネジメントの原理原則をPDF17ページにググっと凝縮！
ぜひ、DL頂き、皆さまの日々のマネジメントに生かしてください！
目次
ロジカルシンキングで重要な3つの推論手法
本章では、ロジカルシンキングによる推論の手法として重要な、以下の3つを解説します。
- 演繹（えんえき）法
- 帰納（きのう）法
- 弁証（べんしょう）法
物事の事実や前提条件をどうやって考えたらよいか分からないという方に特におすすめの手法です。
演繹法とは
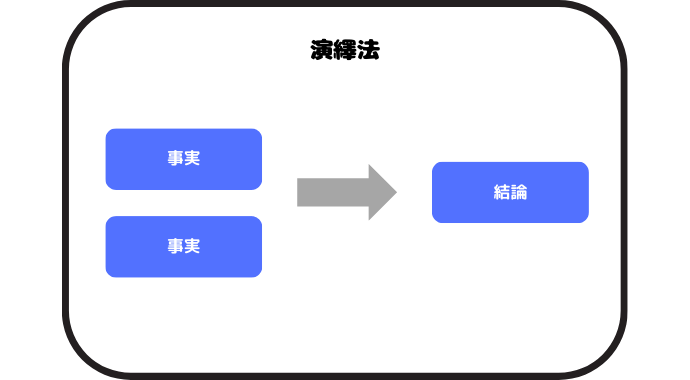
演繹法とは、一般的な考え方やルールなどの前提から個別的な結論を得るというロジカルシンキングの手法のひとつです。
読み方は「えんえきほう」となります。
演繹法には、以下のような「三段論法」という一般的な代表例があります。
- 「木にみかんがなっている」
- 「木になっている果実はフルーツである」
- 「みかんはフルーツである」
図や以上のような例のように、二つの前提から結論を導き出すのが三段論法です。
他にも、以下のような三段論法の一種である「単純三段論法」と呼ばれる論法もあります。
- 「すべての人間は死ぬ」
- 「ゆえに、私は死ぬ」
三段論法と比べると中間項が省略されていますが、私は人間であるという前提が暗黙的に含まれているのです。
演繹法は仕事で物事を判断、意思決定するとき、提案するとき、評価するときなどに活用でき、使用頻度の高い手法といえます。
帰納法とは
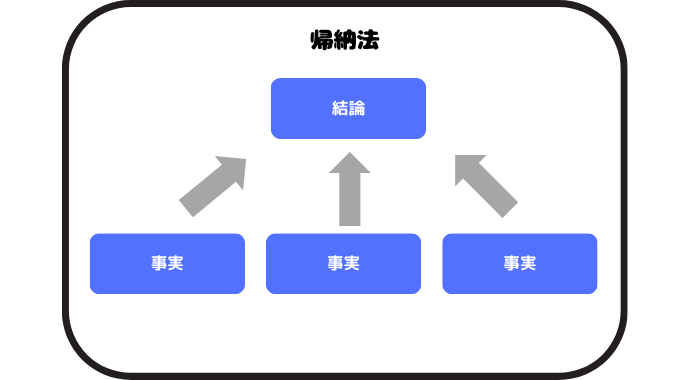
帰納法とは、個別的な事実から一般的な結論を導くロジカルシンキングの推論手法のひとつです。
以下は、帰納法の例です。
- 「りんごはフルーツである」「バナナはフルーツである」「サクランボはフルーツである」
- 「木になっている果実はフルーツである」
図のように、複数の個別的な事実から一般的な結論を推定する形で出していることが分かります。
このとき、りんご・バナナ・サクランボにはフルーツという共通点があります。
なお、演繹法なら前提条件が正しければ結論も正しくなりますが、帰納法は前提が正しくても結論が正しくなるとは限りません。
しかし、過去の経験やデータなどから共通点を見つけ推論できる帰納法は、ビジネスシーンでも活用できる推論方法といえます。
弁証法とは
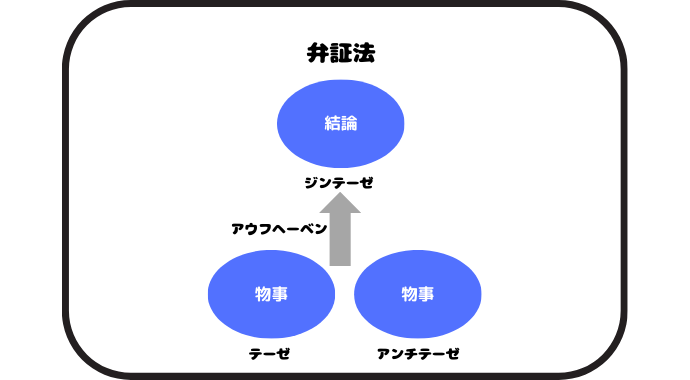
弁証法とは、対立や矛盾する二つの物事（テーゼとアンチテーゼ）を掛け合わせる（アウフヘーベン）ことで、より高次なもの（ジンテーゼ）を生み出す考え方で、哲学です。
ソクテラスの時代に生まれた弁証法は、ヘーゲルによって再発見され、経済学者であるマルクスが定式化させました。
弁証法の例として有名なものに、ホットドッグがあります。
ソーセージとパンを別々に食べるのではなく、テーゼ（ソーセージ）とアンチテーゼ（パン）を組み合わせることで、ホットドッグ（ジンテーゼ）としての新たな価値が生まれました。
ジンテーゼであるホットドッグをテーゼとして新たなアンチテーゼを組み合わせればさらに新たなジンテーゼが生まれます。
弁証法はさまざまな角度から答えを導き出すことができ、次々と発想を発展させられる手法です。
演繹法の特徴
演繹法には、以下のような特徴があります。
- 正しい前提条件から始めれば、必然的に正しい結論が得られる
- 数学や論理学でよく使われている
- 三段論法という形式で使われることが多い
2つ目、3つ目の特徴は「演繹法とは」や「演繹法におけるロジカルシンキングの手順」の章で解説した通りです。
1つ目の特徴については、例を挙げて解説します。
（例）
- 人は必ず死ぬ（事実）
- ソクラテスは人である（事実）
- ソクラテスは必ず死ぬ（結論）
演繹法は、前提条件にとって意味のある結論が必ず出るようになっています。
前提条件が正しければ結論も必ず正しくなる、というのが演繹法の特徴です。
もし、上記例の結論が間違っているとしたら、前提条件である1と2の事実は「死なない人もいる」や「ソクラテスは人でない」などのようになります。
以上のように、結論が間違っているのなら前提に必ず間違いが含まれているのです。
演繹法と帰納法の違いを分かりやすく解説
演繹法と帰納法には、それぞれ以下のような違いがあります。
- 推論の際に、抽象度を下げていくのが「演繹法」、抽象度を上げていくのが「帰納法」
- 前提が正しいと結論も正しくなるのが「演繹法」、前提が正しくても結論が正しいとは限らないのが「帰納法」
- 結論から新しい知識を得られないのが「演繹法」、結論から新しい知識を得られるのが「帰納法」
- 一貫性のある物事に適しているのが「演繹法」、統計や分析に適しているのが「帰納法」
演繹法は、一般的な事実（普遍的命題）から個別的な結論（個別的命題）を導き出す方法です。
一方で帰納法は、個別的な事実から一般的な結論を導き出す方法です。
演繹法と帰納法が効果を発揮する場面にも違いがありますが、帰納法で導かれた結論が演繹法の前提条件に用いられることも多々あります。
実際にビジネスシーンでロジカルシンキングを活用する際には、演繹法と帰納法の両方の推論を用いて進めていくとよいでしょう。
演繹法におけるロジカルシンキングの手順
これまでも演繹法におけるロジカルシンキングの手順である「三段論法」を説明してきました。
ビジネスシーンでもよく使われる演繹法でどのように物事を考えたらよいか、具体的に解説していきます。
- 前提条件となる事実を用意する
- 前提条件にあてはまる事実を推論する
- 前提条件とあてはめた事実から結論を導く
1.前提条件となる事実を用意する
まずは、前提条件を用意します。
演繹法は、前提条件が正しければ結論も正しくなるという特徴があるため、正しい前提条件を用意することが大切です。
前提条件となる事実として考えられるものは以下の通りです。
- プロジェクトや会議などの目的
- 因果関係
- 実証済みの理論（セオリー）
- 基準
- 法則
- 方針
- 価値観や文化 など
たとえば、「○○という策を打ち出したら購入者の80%が女性となった」という過去のデータがあれば、すでにある因果関係として前提条件となります。
2.前提条件にあてはまる事実を推論する
次に、用意した前提条件から結論を導くために、あてはまる事実を推論します。
1で挙げた前提条件の例をもとに考えてみましょう。
前提条件が「○○という策を打ち出したら購入者の80%が女性となった」なので「今度の新商品の購入層は男女比2:8」という事実をあてはめられます。
ポイントは「今度の新商品の購入層は男女比2:8」という事実が、直感や主観的なものではなく、客観的な事実でなければならないということです。
さらに、前提条件と客観的な事実の間には論理的な関係がある事が求められます。
3.前提条件とあてはめた事実から結論を導く
最後に、用意した前提条件とあてはめた事実から結論を導いていきます。
- 前提条件：○○という策を打ち出したら、購入者の80%が女性となった
- 前提条件にあてはめた事実：今度の新商品の購入層は男女比2:8
- 結論：よって、今度の新商品のPRに○○という策を打ち出したらよい
また、結論から「そうすれば今度の新商品の購入層は男女比2:8になる」とも言え「なぜ新商品のPRに○○という策なのか？」の根拠ともなります。
このように演繹法は「前提条件を用意する」→「前提条件に事実をあてはめて考える」→「結論」という1〜3の手順で物事を考えられる手法となっています。
演繹法の具体例
演繹法は、日常生活をはじめ、ビジネスシーンでも使用頻度の高いロジカルシンキングの手法です。
本章では、演繹法の具体例として以下の3つを紹介します。
- ビジネスシーンでの例
- 日常生活での身近な例
- 面白い例
ビジネスシーンでの例
ビジネスシーンで演繹法は、契約や規則、データ、分析などを前提として具体的な判断や行動を決めるときなどに使えます。
ビジネスシーンで活用できる演繹法として、たとえば以下のような例が考えられます。
- 契約によると、納品が遅れた場合には違約金が発生する。
- 私たちは納品が遅れた。
- ゆえに、私たちは違約金を支払わなければならない。
- データの分析によれば、この市場の需要は年々減少している。
- 私たちはこの市場に参入しようとしている。
- ゆえに、私たちは利益を得るのが難しいようだ。
実際には、例のような簡単な状況や要素ではなく、より複雑な状況や要素を求められるでしょう。
しかし、演繹法は論理的で明確な推論を行うために有効なツールであることに間違いありません。
日常生活での身近な例
日常生活での身近な例として、「モードゥストレンス」と「モードゥスポネンス」を用いた例を紹介します。
「モードゥストレンス」と「モードゥスポネンス」は演繹法の一種で、条件文を使った論証の方法です。
「モードゥストレンス」は後件否定、「モードゥスポネンス」は、前件肯定とも呼ばれます。
- 具体例1（モードゥストレンス）：もし雨が降っていたら、道が濡れている。道は濡れていない。ゆえに、雨は降っていない。
- 具体例2（モードゥスポネンス）：もし彼女が花粉症なら、くしゃみをするだろう。彼女は花粉症だ。ゆえに、彼女はくしゃみをする。
面白い例
日本経済新聞社がnote上で運営している投稿マガジン「日経COMEMO（コメモ）」には、「鬼滅の刃」を例にして演繹法を説明している記事があります。
記事のなかで演繹法の説明に使われている例は以下の三段論法です。
- （大前提）あらゆる鬼は人に危害を加える存在である
- （小前提）竈門禰󠄀豆子は鬼である
- （結論）竈門禰󠄀豆子は人に危害を加える存在である
引用：鬼滅の刃で理解する、帰納法と演繹法を用いた仮説の作り方｜松本健太郎
「鬼滅の刃」を知っている人であれば演繹法の具体例として面白いと感じるのではないでしょうか。
帰納法の例題
本章では、帰納法の例題を2つ紹介します。
どのような結論が導けるか、考えてみてください。
- 例題1：「コンビニ各社のいれたてコーヒーが人気」→「異業種の店舗でも、いれたてコーヒーを提供し集客がアップ」→「？」
引用：大嶋祥誉「マッキンゼー流入社1年目ロジカルシンキングの教科書」(2014年)p132-134
- 例題2：「A社から支払いの先延ばしがあった」→「A社は新製品が出ていない」「A社の従業員が多く辞めている」→「？」
例題1から導ける結論として考えられるのは「いれたてコーヒーが集客の武器になる」です。
例題2から導ける結論として考えられるのは「A社は経営難に陥っている」です。
しかし、帰納法はこれまで解説してきたように前提条件が正しくても結論が正しいとは限りません。
新たな発想を生み出したいとき、自身の観察力や想像力を用いて帰納法を活用するのがおすすめです。
演繹法や帰納法を意識的に取り入れよう
本記事では、演繹法と帰納法の違いや具体例、演繹法の手順などを解説しました。
演繹法は、一般的な考え方やルールなどの前提から個別的な結論を出す手法です。
確実な推論ですが、前提が正しくなければなりません。
一方で、帰納法は確率的な推論ですが、全体を代表するような事実が必要です。
演繹法は問題解決や商品開発などに役立つツールです。
ぜひ自分の仕事や日常生活に活用してみてください。
株式会社識学 代表取締役社長 安藤広大の執筆した書籍『数値化の鬼』が、なんと発売後 約１か月で１２万部を突破しました！
この感謝を皆様にも還元すべく、株式会社識学では、『数値化の鬼』の図解解説資料を作成いたしました！
一度書籍をお読みになった方も、まだお手元にない方もどなたでも満足いただける完成度となっています！
眺めるもヨシ、印刷して目の付くところに飾るもヨシ、使い方は自由自在！
是非、こちらからDLしてくださいね！
